Neutrino Oscillations and Neapolitan Ice Cream
Neutrino oscillations are a topic of great importance to several modern physics questions. Yet, the concept of something described as a 'fundamental block of reality' transforming can be very strange. One of the greatest difficulties with quantum mechanics is how abstract things get.
As an example, electroweak unification is spontaneously broken below a certain energy level, and physicists describe the degree to which the breaking occurs with something called the Weinberg angle. So, what is this angle relating? Since it is an angle in a purely mathematical space, it relates two entirely nonphysical concepts. It is so important to recognize that frequently quantum mechanical concepts are so deep in the weeds that it's hard to remember that the language used refers to mathematical objects.
So: how do we fix this sort of issue? I think one option, when done with care is to make it something you could physically picture.
Humans and Taste
From my experience, one of the joys of combining food comes about from how flavors and textures can mix and create something seen as greater than the sum of its parts. While quantum states need to be 'on a complete basis', so it's not reasonable to see them as "greater than the sum of its parts", I think this is a decent starting point.
Author's Note: This may also be influenced by how flavors will combine to create another flavor that exists on its own for me, so if you have a hard time with the picture, it's in part because I don't know how common that is.
Basics of Superposition
When physics students are first taught quantum mechanics in a quantum mechanics class, one of the common methods through which it's taught is a conceptual version of the Stern-Gerlach experiment.
The actual Stern-Gerlach experiment was performed by Walther Gerlach in 1922, where a magnetic field is imposed in a uniform manner along one direction, and silver atoms are fired from a furnace which prepares them in random, but distinct states. Physicists knew that there was a mode by which magnetism could affect fundamental particles, but until this experiment, it was thought that it should produce a spectrum of results on the final plate the atoms hit.
The experiment showed that silver atoms only have two options for what we now call 'spin'. By the way, it's only called this because it is mathematically identical to classical angular momentum, but by being an intrinsic property, needed to be distinguished from orbital angular momentum. This 'spin', for a fundamental particle like the electron, has the possible values 1/2 and -1/2.
With the appropriate assembly of a series of oriented magnetic fields in the Stern-Gerlach experiment, it becomes possible to prepare silver atoms that have the only expression of their 'spin' mixed. You lose the ability to deterministically know, if you pick a random particle if its spin will definitively be 1/2 or -1/2. For example, when an individual particle interacts with something outside its quantum system, it could be that three out of four times, it interacts as if the particle has a spin of 1/2 and one out of four times it interacts as if its spin is -1/2. The only requirement is that the total probability of all possible states is 1. In this case, it means that if you checked a particle, it would necessarily be either 1/2 or -1/2, and you could not have a particle that is 100% 1/2 and 100% -1/2. If it's 100% 1/2, it has to be 0% -1/2.
This is the interference effect that is special in quantum mechanics. It's observable with light on the macro-scale, but all matter has these interference effects, just like light! We just can't tell since we exist at the macroscopic level, at energy regions far above the regime where these effects matter and occur for anything we can observe day to day. This even extends to the Stern-Gerlach experiment itself. Your finger has 10²³ atoms in it. Even the Stern-Gerlach experiment, when one demonstrates that the silver atoms can have a nontrivial but determined proportion of spin-1/2 states, it is never truly one silver atom being considered. This is rhetorically useful, but it's almost always infeasible to think about one particle doing anything in quantum mechanics uniquely at the end of the day.
Now, onto pinker pastures!
Eigenstates
What I'm told is the dreaded prefix of any non-mathematician who had to take an introduction to linear algebra course: Eigen-. The prefix means, approximately, "own" or "characteristic". In an introductory course, it's used with eigenvalues and eigenvectors of a matrix.
For a given matrix A, assuming it has eigenvalues, the eigenvectors are the vectors which, when multiplied by the matrix A, do not transform. They preserve their value, which as vectors, means they do not change magnitude or direction. This is the important element of their behavior, and is the reason why they are called "characteristic"! They can be derived from the matrix A itself, and characterize the nature of whatever transformation A does on a vector by representing what it doesn't transform.
Quantum states are represented by a vector in an arbitrary mathematical space. [It's more complicated than this, but this is the important element] Physical properties and values can be represented by operators, which can take mathematical form as matrices, which have eigenvalues and eigenvectors. Eigenstates are these eigenvectors.
The state which does not transform under a given transformation (operator) is usually the state with which you want to solve a problem using that transformation, because when an operator acts on a state which is an eigenstate for that operator, the operator just returns the associated eigenvalue of that eigenstate. The specifics of this are not important, and depicted in the image below. The important part is that eigenstates are untransformed by an operator.
If ψ is an eigenstate of the operator Â, then the equation below must be true.
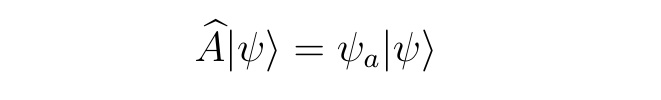
If ψ is not an eigenstate of the operator Â, then the generic equation instead appears as
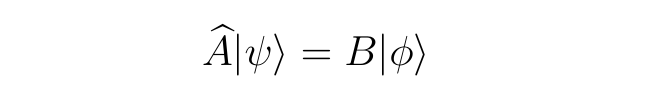
where ϕ is a state which has been modified through one of several means depending on the nature of the operator Â, and the constant B normalizes this.
Neutrinos
Switching streams for a moment, neutrinos are often talked about as one entity, but there are actually three distinct flavors of neutrinos. Each one is paired with one of the three charged leptons, the electron, the muon, and the tau. The muon and tau are heavier fundamental analogues of the electron. Both carry the same amount of fundamental amount of charge the electron has. None of these particles interact with the strong force, and importantly, neutrinos do not interact with the electromagnetic force. At. All. The charged leptons absolutely do, as that's what gives us physical form, but neutrinos do not. This is why you may have seen them described as 'warm dark matter', or 'ghost particles'!
Feynman Diagrams
Most people have seen Feynman diagrams. They're an easy thing to throw up in the background on a blackboard when you're trying to make a scientist seem smart, since they are mostly just squiggly lines.
Feynman diagrams visually represent how interactions proceed when looking at fundamental particles. It's important to know that the interior of a diagram is a black box. Any diagram that obeys the rules for appropriately connecting lines, but has the same external lines, contributes to the overall observable quantification of the same interaction. Since the diagrams can be assembled like Legos, as they simply represent more foundational math, it's possible to assemble endlessly more complex diagrams with the same external lines. This would be obnoxious, but quantum electrodynamics, and weak force processes, are both perturbative. This means that as the number of vertices increases, the contribution to the overall drops quite starkly.
Neutrinos only interact with the weak force, so when constructing Feynman diagrams, they should only couple to weak boson vertices. Also in Feynman diagrams, charge and fermion lines must flow continuously through the diagram.
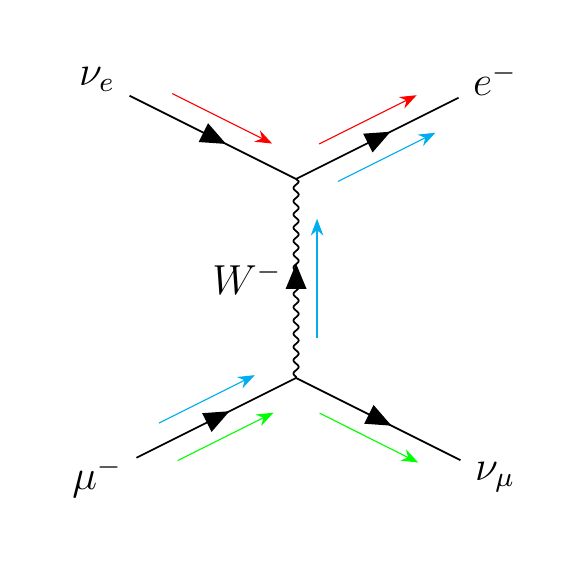
In the image above, the red arrows represent the continuous flow of 'electron' flavor, the cyan arrows represent the continuous flow of -1 charge, and the green arrows represent the continuous flow of the 'muon' flavor.
The W± bosons indicate a change from a charged lepton into its paired neutrino flavor, while the Z⁰ boson preserves neutrino or lepton nature. Remember that for an eigenstate, an operator acting on it does not change the state. The fact that neutrinos 'transform' into charged leptons upon interacting with the W± bosons, and vice versa as needed, contributes to the notion that the W± (and Z) bosons couple to a "weak flavor eigenstate", which means that the flavor, electron, muon, or tau, is unaffected by interaction with the weak boson. In other words, an electron neutrino, simply by interaction with a charged weak boson, cannot suddenly become a muon in one point interaction.
Neapolitan Ice Cream
So, with all of that prefacing out of the way: Neapolitan ice cream.
Imagine the electron, muon, and tau flavors as the vanilla, chocolate, and strawberry ice creams in a container of magically refilling Neapolitan ice cream. These are the flavors which make up the "complete space of Neapolitan ice cream". Interacting with a weak boson is analogous to taking a spoon and eating a component of one of the three flavors. Eating strawberry ice cream from it is like a tau neutrino interacting with a weak boson. The fact that it magically refills ensures completeness of your ice cream space.
The vanilla, chocolate, and strawberry dichotomy makes sense when consuming ice cream directly [we are assuming that only one flavor of ice cream can be tasted at a time]. They could be called the "spoon-to-mouth eigenstates". However, when the ice cream container is closed, analogous to free particles traveling, it could be the case that the flavors which define the Neapolitan ice cream are no longer vanilla, chocolate, and strawberry. Perhaps, when the ice cream container is closed, the good flavor descriptions are vanilla bean [trust me, it's different], pistachio, and cherry, our "traveling closed container eigenstates".
When you open it and eat the ice cream–clearly an instantaneous process, if you ask me–you only taste the ice cream as vanilla, chocolate, or strawberry, despite what flavors they are when the container is closed.
Neutrino oscillations pose that, when the ice cream container is closed—that is to say, they are traveling in free space without interactions—the three neutrino flavors "mix" together, and upon interacting later, a number of neutrinos can interact as if they were in different ratios than the initial group. This is as if, on initially opening the ice cream container, it was 33% vanilla, 33% chocolate, and 33% strawberry. Then it was closed, and when reopened it later, the mixture was now something like 50% vanilla, 30% chocolate, 20% strawberry.
Using the physics language, the "spoon-to-mouth eigenstates" of the vanilla, chocolate, strawberry flavor group are the "weak flavor eigenstates" of the Neapolitan ice cream. They are distinctly not the "closed container traveling eigenstates". The reason the ratios of vanilla, chocolate, and strawberry cannot change when you're tasting them is because those are the eigenstates when you taste them. You will not see chocolate change into strawberry when you taste it, because it's an eigenstate of your spoon.
The vanilla bean, pistachio, cherry group is the "free particle/closed container traveling eigenstate" group, because if you framed your Neapolitan ice cream in these flavors, it could be the case that you put pistachio ice cream on your spoon, and it entered your mouth as cherry, because it is not the "spoon-to-mouth eigenstate". Yet, when you close the container, if the ratio is 30% vanilla bean, 35% pistachio, 35% cherry? It will be that same ratio when you reopen the container. They will not change like the vanilla, chocolate, strawberry ice cream set would have.
Back to Neutrino Oscillations
The reason we know neutrinos have mass, that the vanilla bean, pistachio, cherry flavor basis exists, is because if the weak particle states, the spoon-to-mouth eigenstates can change their relative proportions in motion, due to the rules of linear algebra and quantum mechanics, there must be a basis in which the fundamental quantities used to picture it, the vanilla bean, pistachio, cherry basis, are invariant.
Without mass, there is no eigenstate to which the coupling could be had for a free particle, at least in the present theory of particle physics. Therefore, if your fundamental vanilla, chocolate, strawberry basis could not be expressed in proportions of vanilla bean, pistachio, and cherry, the vanilla, chocolate, and strawberry flavors would never mix, and the spoon-to-mouth eigenstates would be the same as the closed container traveling eigenstates. You would never see the vanilla, chocolate, strawberry ratio fluctuate without the coupling to an underlying unobserved basis, such as the vanilla bean, pistachio, cherry basis.
Importantly, the reason this underlying basis is not tangibly useful as a picture other than explaining the relation and oscillations between the preexisting vanilla, chocolate, and strawberry flavors, is because for neutrinos, they cannot be interacted with outside of the weak interaction, unlike every other fundamental particle. Quarks interact with gluons in their versions of the vanilla bean, pistachio, cherry basis, and electrons, muons, and tau leptons do the same with photons.
Thus, because the standard representation of a state is chosen based on the useful eigenstate, and physicists did not know about neutrino oscillations until well after the formalization of neutrinos into the standard model. Thus, with the only useful eigenstates being the weak interaction eigenstates, the flavors in the standard model were chosen accordingly. If, say one only carried their Neapolitan ice cream in a glass tub that they never ate from, then the vanilla bean, pistachio, cherry basis would be the logical choice. However, I think most people can agree that ice cream is meant for eating, rather than observing.
A Fun Fact to Finish:
Neapolitan ice cream being called as such is due to its association with Naples (the name then not surprising given Neapolitan being the English exonym for Naples), despite instead likely being first originated by the chef of a Prussian household. As for why it's associated with Naples, it at some point made it down there, at which point Italians immigrated to the US, and sold various sets of combinations of three flavors [Weir] (Sidenote: an association was formed between Hokey Pokey and ice cream through Italian vendors in England [Weir]). One of the combinations that likely contributed to the misnomer for the ice cream was a combination of pistachio, vanilla, and cherry to match the Italian flag, but the vanilla, chocolate, strawberry of today likely came about through the joint popularity of those three flavors. [Weir]
[Weir] Ice Creams, Sorbets & Gelati: The Definitive Guide. Caroline Weir, Robin Weir.
P.S. If this post is still up, it means I likely haven't gotten an email from a theoretical physicist explaining to me why I'm wrong to call the neutrino masses vanilla, chocolate, and strawberry.
